Cylindrical T-matrices

Here, we will cover cylindrical T-matrices, which are distinguished from the more conventional (spherical) T-matrices through the use of vector cylindrical functions instead of vector spherical functions. These waves are parametrized by the z-component of the wave vector \(k_z\), that describes their behavior in the z-direction \(\mathrm e^{\mathrm i k_z z}\), and the azimuthal order \(m\), that is also used in vector spherical functions. Furthermore, there modes of well-defined parity and helicity are available.

The cylindrical T-matrices are suited for structures that are periodic in one dimension (conventionally set along the z-axis). Similarly to T-matrices of spheres that contain the analytically known Mie coefficients, the cylindrical T-matrices for infinitely long cylinders can also be calculated analytically.

Another similarity to spherical T-matrices are the possibilities to describe clusters of objects in a local and global basis and to place these objects in a lattice. The lattices can only extend in one and two dimensions; the z-direction is implicitly periodic already.

(Infinitely long) Cylinders

The first simple object, for which we’ll calculate the cylindrical T-matrix is an infinitely long cylinder. (Similar to the case of spheres and T-matrices those cylinders could also have multiple concentric shells.) Due to the rotation symmetry about the z-axis this matrix is diagonal with respect to m and due to the translation symmetry it is also diagonal with respect to kz.

k0s = 2 * np.pi * np.linspace(1 / 6000, 1 / 300, 200)
materials = [treams.Material(16 + 0.5j), treams.Material()]
mmax = 4
radius = 75
kzs = [0]
cylinders = [treams.TMatrixC.cylinder(kzs, mmax, k0, radius, materials) for k0 in k0s]

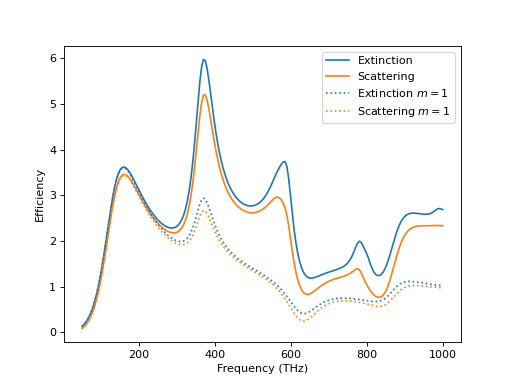
For such infinitely long structures it makes more sense to talk about cross width instead of cross section. We obtain the averaged scattering and extinction cross width by

xw_sca = np.array([tm.xw_sca_avg for tm in cylinders]) / (2 * radius)
xw_ext = np.array([tm.xw_ext_avg for tm in cylinders]) / (2 * radius)

Again, we can also select specific modes only, for example the modes with \(m = 0\).

cwb_mmax0 = treams.CylindricalWaveBasis.default(kzs, 0)
cylinders_mmax0 = [tm[cwb_mmax0] for tm in cylinders]
xw_sca_mmax0 = np.array([tm.xw_sca_avg for tm in cylinders_mmax0]) / (2 * radius)
xw_ext_mmax0 = np.array([tm.xw_ext_avg for tm in cylinders_mmax0]) / (2 * radius)

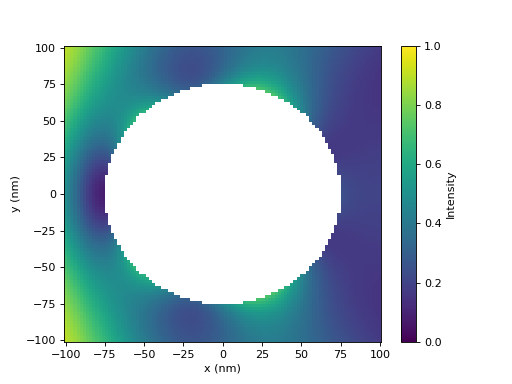
to calculate their cross width. Evaluating the field intensity in the x-y-plane is equally simple.

cwb_mmax0 = treams.CylindricalWaveBasis.default(kzs, 0)
cylinders_mmax0 = [tm[cwb_mmax0] for tm in cylinders]
xw_sca_mmax0 = np.array([tm.xw_sca_avg for tm in cylinders_mmax0]) / (2 * radius)
xw_ext_mmax0 = np.array([tm.xw_ext_avg for tm in cylinders_mmax0]) / (2 * radius)

(Source code)

(png, hires.png, pdf)

(png, hires.png, pdf)

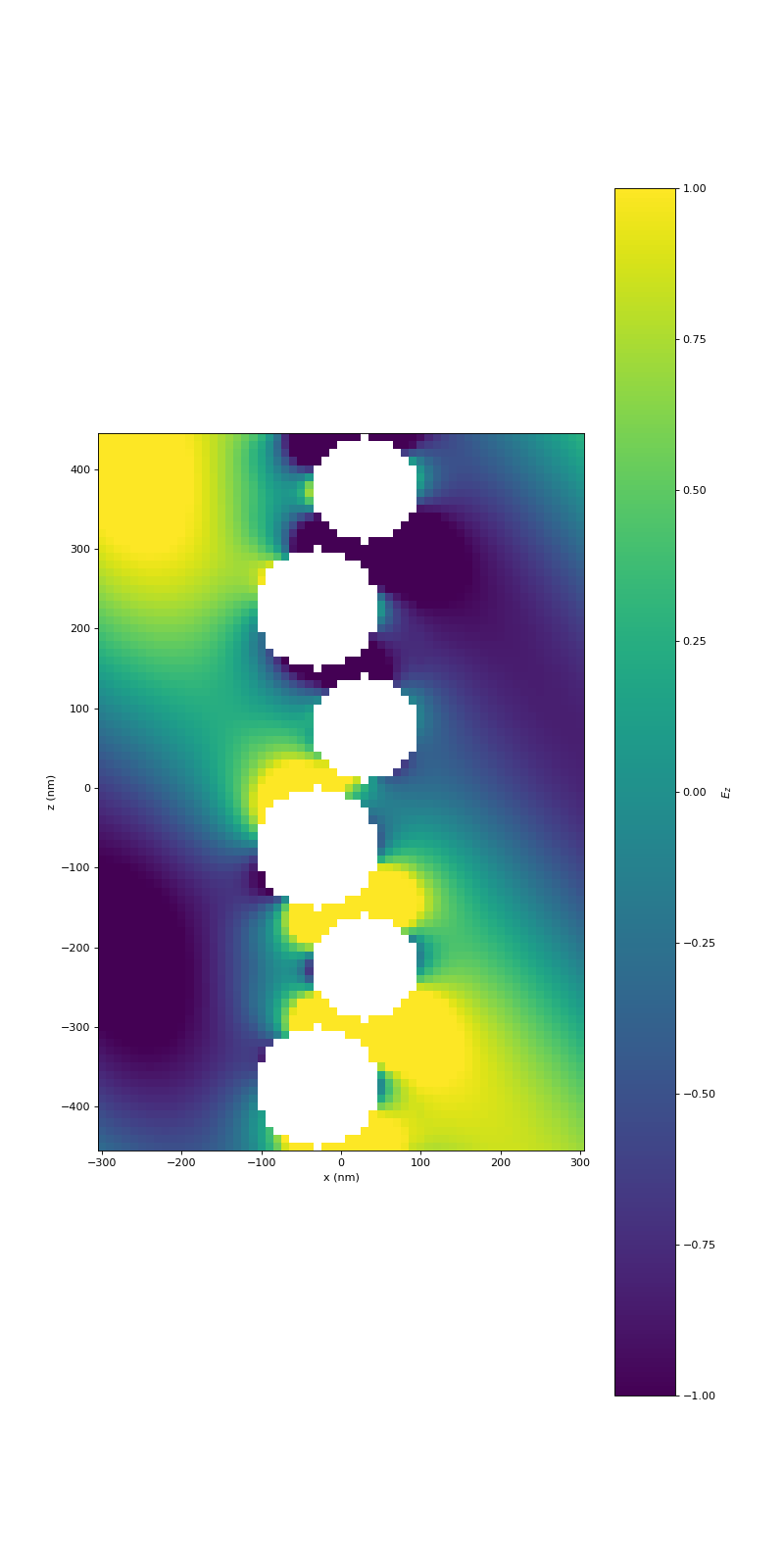
Cylindrical T-matrices for one-dimensional arrays of spherical T-matrices

For our next example we want to look at the system of spheres on a one-dimensional lattice again (One-dimensional arrays (along z)). They fulfil all properties that define structures where the use of cylindrical waves is beneficial, namely they have a finite extent in the x-y-plane and they are periodic along the z-direction.

So, the initial setup of our calculation starts with spheres in the spherical wave basis and place them in a chain. This is the same procedure as in One-dimensional arrays (along z).

k0 = 2 * np.pi / 700
materials = [treams.Material(-16.5 + 1j), treams.Material()]
lmax = mmax = 3
radii = [75, 65]
positions = [[-30, 0, -75], [30, 0, 75]]
lattice = treams.Lattice(300)
kz = 0.005

spheres = [treams.TMatrix.sphere(lmax, k0, r, materials) for r in radii]
chain = treams.TMatrix.cluster(spheres, positions).latticeinteraction.solve(lattice, kz)

Next, we convert this chain in the spherical wave basis to a suitable cylindrical wave basis.

bmax = 3.1 * lattice.reciprocal
cwb = treams.CylindricalWaveBasis.diffr_orders(kz, mmax, lattice, bmax, 2, positions)
chain_tmc = treams.TMatrixC.from_array(chain, cwb)

We chose to add the first three diffraction orders (plus a 0.1 margin to avoid problems with floating point comparisons).

Finally, we set-up the illumination and calculate the scattering with the usual procedure.

inc = treams.plane_wave(
    [np.sqrt(k0 ** 2 - kz ** 2), 0, kz],
    [np.sqrt(0.5), np.sqrt(0.5)],
    k0=chain.k0,
    material=chain.material,
)
sca = chain_tmc @ inc.expand(chain_tmc.basis)

We evaluate the fields in two regions. Outside of the circumscribing cylinders we can use the fast cylindrical wave expansion. Inside of the circumscribing cylinders but outside of the spheres we can use the method of One-dimensional arrays (along z).

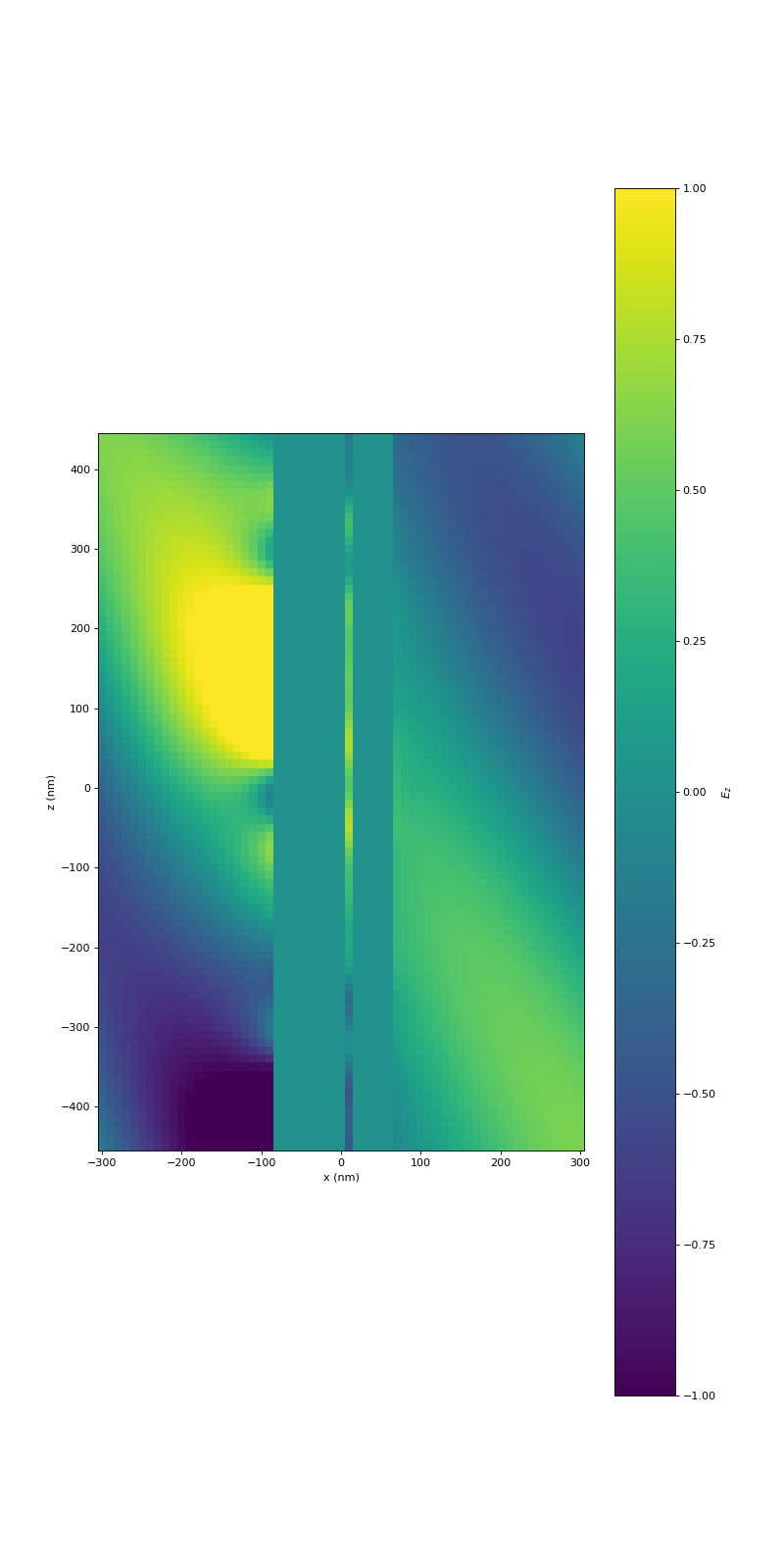
Finally, we can plot the results. To illustrate the periodicity better, three unit cells are shown.

(Source code, png, hires.png, pdf)

Clusters

Similarly to the case of spheres we can also calculate the response from a cluster of objects. For the example want to simulate a cylinder together with a chain of spheres in the cylindrical wave basis as described in the previous section.

So, we set up first the spheres in the chain and convert them to the cylindrical wave basis as before

k0 = 2 * np.pi / 700
materials = [treams.Material(-16.5 + 1j), treams.Material()]
lmax = mmax = 3
radii = [65, 55]
positions = [[-40, -50, 0], [40, 50, 0]]
lattice = treams.Lattice(300)
kz = 0.005

sphere = treams.TMatrix.sphere(lmax, k0, radii[0], materials)
chain = sphere.latticeinteraction.solve(lattice, kz)
bmax = 3.1 * lattice.reciprocal
cwb = treams.CylindricalWaveBasis.diffr_orders(kz, mmax, lattice, bmax)
chain_tmc = treams.TMatrixC.from_array(chain, cwb)

Then, we create the cylinder T-matrix in the cylindrical wave basis

cylinder = treams.TMatrixC.cylinder(np.unique(cwb.kz), mmax, k0, radii[1], materials)

Finally, we construct the cluster and let the interaction be solved

cluster = treams.TMatrixC.cluster([chain_tmc, cylinder], positions).interaction.solve()
inc = treams.plane_wave(
    [np.sqrt(k0 ** 2 - kz ** 2), 0, kz],
    [np.sqrt(0.5), np.sqrt(0.5)],
    k0=chain.k0,
    material=chain.material,
)
sca = cluster @ inc.expand(cluster.basis)

and we solve calculate the scattered field coefficients, whose field representation we then plot

(Source code, png, hires.png, pdf)

One-dimensional arrays (along the x-axis)

Now, we take the chain of spheres and a cylinder and place them in a grating structure along the x-direction. We start again by defining the parameters and calculating the relevant cylindrical T-matrices.

k0 = 2 * np.pi / 700
materials = [treams.Material(-16.5 + 1j), treams.Material()]
lmax = mmax = 3
radii = [65, 55]
positions = [[-40, -50, 0], [40, 50, 0]]
lattice_z = treams.Lattice(300)
lattice_x = treams.Lattice(300, "x")
kz = 0.005

sphere = treams.TMatrix.sphere(lmax, k0, radii[0], materials)
chain = sphere.latticeinteraction.solve(lattice_z, kz)
bmax = 1.1 * lattice_z.reciprocal
cwb = treams.CylindricalWaveBasis.diffr_orders(kz, mmax, lattice_z, bmax)
kzs = np.unique(cwb.kz)
chain_tmc = treams.TMatrixC.from_array(chain, cwb)
cylinder = treams.TMatrixC.cylinder(kzs, mmax, k0, radii[1], materials)

Next, we create the cluster and, as usual, let it interact within a lattice of the defined periodicity. Then, it’s simple to calculate the scattering coefficients.

cluster = treams.TMatrixC.cluster(
    [chain_tmc, cylinder], positions
).latticeinteraction.solve(lattice_x, 0)
inc = treams.plane_wave(
    [0, np.sqrt(k0 ** 2 - kz ** 2), kz],
    [np.sqrt(0.5), -np.sqrt(0.5)],
    k0=chain.k0,
    material=chain.material,
)
sca = cluster @ inc.expand(cluster.basis)

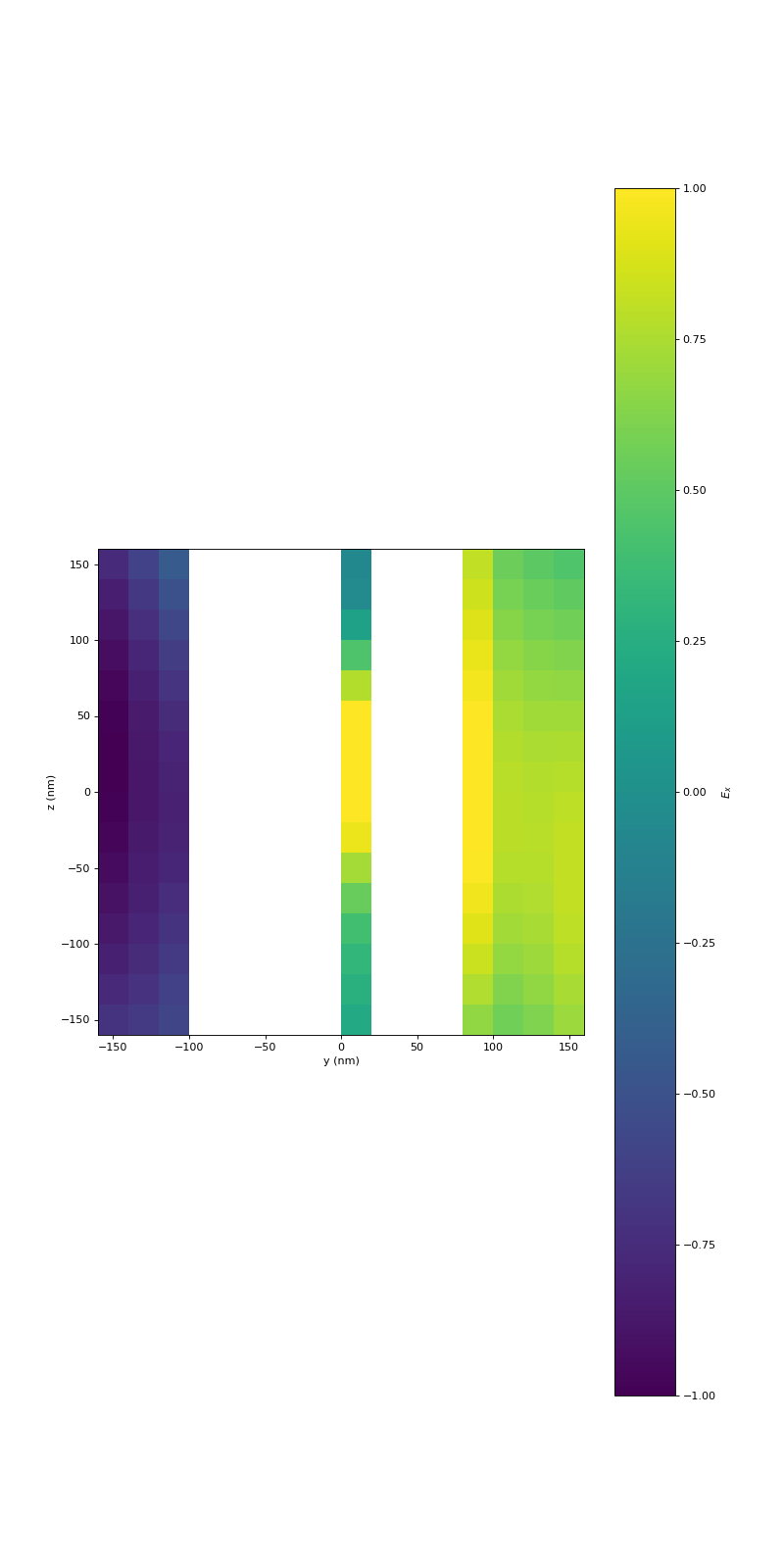
In the last step, we want to sum up the scattered fields at each point in the probing area

grid = np.mgrid[0:1, -150:150:16j, -150:150:16j].squeeze().transpose((1, 2, 0))
ex = np.zeros_like(grid[..., 0])
valid = cluster.valid_points(grid, radii)
vals = []
for i, r in enumerate(grid[valid]):
    cwb = treams.CylindricalWaveBasis.default(kzs, 1, positions=[r])
    field = sca.expandlattice(basis=cwb).efield(r)
    vals.append(np.real(inc.efield(r)[0] + field[0]))
ex[valid] = vals
ex[~valid] = np.nan

and plot the results.

(Source code, png, hires.png, pdf)

Two-dimensional arrays (in the x-y-plane)

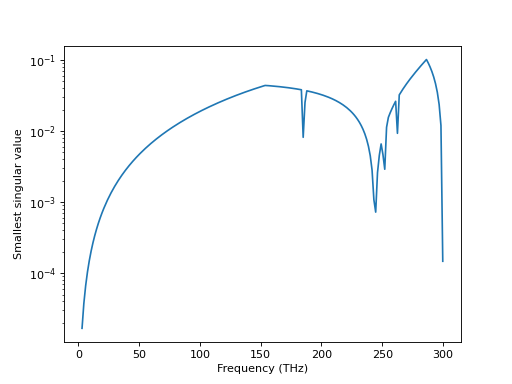
As last example, we want to examine a structure that is a photonic crystal consisting of infinitely long cylinders in a square array in the x-y-plane.

k0s = 2 * np.pi * np.linspace(0.01, 1, 200)
materials = [treams.Material(12.4), treams.Material()]
mmax = 3
radius = 0.2
lattice = treams.Lattice.square(0.3)
kpar = [0, 0, 0]

res = []
for k0 in k0s:
    cyl = treams.TMatrixC.cylinder(kpar[2], mmax, k0, radius, materials)
    svd = np.linalg.svd(cyl.latticeinteraction(lattice, kpar[:2]), compute_uv=False)
    res.append(svd[-1])

fig, ax = plt.subplots()
ax.set_xlabel("Frequency (THz)")
ax.set_ylabel("Smallest singular value")
ax.semilogy(299.792458 * k0s / (2 * np.pi), res)
fig.show()

Similarly to the case of spheres and a three-dimensional lattice, we can check the smallest singular value.

(Source code, png, hires.png, pdf)